Tolking av prøveresultater

​Laboratorieprøver blir hovedsakelig bestilt ved to ulike typer av problemstillinger:

• Diagnostikk: Vi ønsker å påvise sykdom eller grad av sykdom
• Kontroll: Vi skal overvåke endringer hos pasienter med kjente tilstander

Dette kapitlet omtaler noen verktøy som er nyttige når vi skal tolke prøveresultater ved diagnostikk og kontroll.

1. Diagnostikk

 Sannsynlighet for sykdom

Hvis vi bestiller laboratorieprøver for å stille en diagnose, betyr det som regel at vi ikke er sikker på diagnosen etter å ha vurdert sykehistorien og utført en klinisk undersøkelse. Men vi har en mistanke om hvilken tilstand pasienten kan ha, og denne mistanken eller sannsynligheten kalles pretestsannsynlighet for sykdom. Den bruker vi, sammen med prøveresultatet, til å finne posttestsannsynlighet. Dette gjør vi etter beste skjønn, men vi kan også gjøre det rent formelt etter følgende formel (1):

post=(S•pre)/[(S•pre)+1-pre]

der post er posttestsannsynlighet, pre er pretestsannsynlighet og S er prøveresultatets sannsynlighetsratio.

Vårt problem som diagnostikere er således todelt. Vi må ha en viss formening om pretestsannsynlighet, basert på sykehistorie og kliniske funn, og vi må bestemme oss for hvilken vekt vi vil tillegge prøveresultatet. Denne vekten kalles sannsynlighetsratio (på engelsk "likelihood ratio").

Generelt gir sannsynlighetsratio lik 1 samme posttest- som pretestsannsynlighet, sannsynlighetsratio mindre enn 1 gir posttestsannsynlighet mindre enn pretestsannsynlighet, og sannsynlighetsratio større enn 1 gir posttestsannsynlighet større enn pretestsannsynlighet, se figur 1.

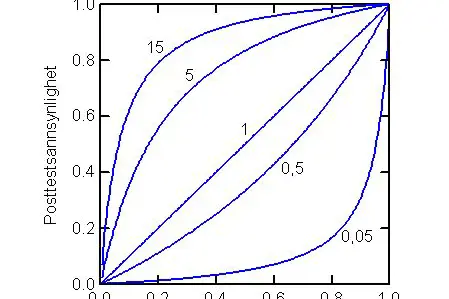
Figur 1  Posttestsannsynlighet plottet som funksjon av pretestsannsynlighet for en del verdier av sannsynlighetsratio

Sannsynlighetsratio er definert slik:

S=(sannsynlighet for prøveresultat gitt sykdom)/(sannsynlighet for prøveresultat gitt ikke-sykdom)

Sannsynlighetsratio er sannsynligheten for å få et visst prøveresultat hos en pasient som har den sykdommen vi mistenker, dividert med sannsynligheten for få akkurat det samme prøveresultatet hos en person som ikke har sykdommen. Hvis prøven bare kan ha positivt eller negativt resultat, blir sannsynlighetsratio for positivt svar lik sensitivitet/(1-spesifisitet) og sannsynlighetsratio for negativt resultat blir (1-sensitivitet)/spesifisitet (1). Sensitivitet er sannsynlighet for positivt prøveresultat hos syke, og spesifisitet er sannsynlighet for negativt prøveresultat hos friske.

Innen medisinsk mikrobiologi og patologi er mange prøveresultater positive eller negative. Slik er det ikke i medisinsk biokjemi, der nesten alle prøveresultater er kvantitative og kan anta uendelig mange verdier. For å ta vare på informasjonen i kvantitative prøveresultater, trenger vi funksjoner for sannsynlighetsratio. Det kan laboratoriet som regel ikke skaffe, men ofte hjelper det å inndele prøveresultatene i grader av patologi. Et eksempel er vist i tabell 1. Diagnosen som skal stilles er jernmangelanemi og testen er s-ferritin, med prøveresultatene inndelt i 6 kategorier. Jo lavere s-ferritin, jo høyere er sannsynlighetsratio. Vi kunne ha omgjort resultatene til positive og negative ved å sette en grense ved for eksempel 15 µg/L. I så fall ville sannsynlighetsratio for et positivt resultat bli 54,5, det samme som for kategorien <=15 µg/L. Men for et negativt resultat ville sannsynlighetsratio bli 0,4, uansett om resultatet var 16 eller 200 mg/L, og det blir misvisende.

Likevel blir både kvantitative og semikvantitative prøveresultater ofte omgjort til positive eller negative i forhold til en grense, trolig fordi det er lettere å forholde seg til bare to mulige resultater. I spesiallitteratur kan vi finne sannsynlighetsratio for en rekke tester i ulike kliniske situasjoner, se for eksempel referanse 3 og 4.

Men i de fleste kliniske situasjoner har vi ikke kunnskap om sannsynlighetsratio for ulike prøveresultater. Da må vi tolke svarene i forhold til referanseområder, og vi må huske at:

Referanseområdet omfatter som regel de sentrale 95% av verdiene som er målt hos personer i en referansepopulasjon, med en verdi fra hver person. I nesten alle sammenhenger dreier dette seg om en populasjon av klinisk friske personer, slik at en frisk person har 95 % sannsynlighet for at prøveresultatet vil være innenfor referanseområdet, 2,5% sannsynlighet for at det vil være lavere enn nedre referansegrense og 2,5 % sannsynlighet for at det vil være over øvre referansegrense

Referanseområdet beskriver kun fordelingen av prøveresultater i referansepopulasjonen - det sier  ingenting om fordelingen av prøveresultater i syke populasjoner. Et prøveresultat som ligger like utenfor referanseområdet, kan være en normal verdi for vedkommende person. Jo lengre fra referanseområdet et resultat ligger, jo sikrere kan vi tolke det som patologisk. Et prøveresultat innenfor referanseområdet utelukker nødvendigvis ikke sykdom.

Trenger vi egentlig noen laboratorieprøve?

Vi beregner sannsynlighet for sykdom for å kunne tilby pasienten riktig behandling. Hvis en behandling for en sykdom er nyttig for syke, men ikke ufarlig for friske, er behandling å foretrekke når sannsynlighet for sykdom overstiger en viss behandlingsterskel (5). Ved sannsynligheter lavere enn denne terskelen bør vi ikke behandle.

I denne sammenheng trenger vi laboratorieprøver bare hvis prøveresultatet vil få oss til å endre valg av behandling. Hvis prøveresultatet ikke får noen konsekvenser, skal vi selvsagt ikke bestille prøven. I figur 2 er dette vist for prøver som bare kan ha positivt eller negativt resultat.

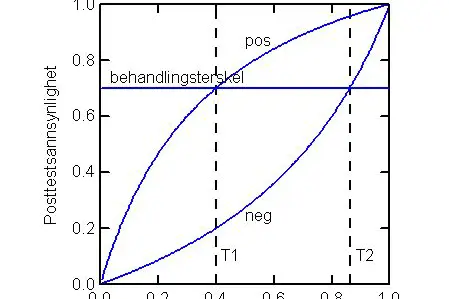
Figur 2  Posttestsannsynlighet plottet som funksjon av pretestsannsynlighet, for positivt (pos) og negativt (neg) prøveresultat. Sensitiviteten er 0,7 og spesifisiteten er 0,8, slik at sannsynlighetsratio for positivt prøveresultat er 3,5 og for negativt resultat 0,375. Behandlingsterskelen er 0,7. Hvis pretestsannsynlighet er under terskelen T1, kommer posttestsannsynlighet ikke over behandlingsterskelen. Hvis pretestsannsynlighet er over terskelen T2, kommer posttestsannsynlighet ikke under behandlingsterskelen. Kun når pretestsannsynlighet ligger mellom tersklene T1 og T2 skal prøveresultatet ha konsekvenser for valget om pasienten skal behandles eller ikke, og kun da er testen indisert.

Vi ser at ved tilstrekkelig lav pretestsannsynlighet for sykdom (mindre enn T1) vil selv et positivt prøveresultat ikke øke sannsynlighet for sykdom til en verdi som ligger over behandlingsterskelen. Hvis vi da behandler på grunnlag av et positivt resultat, gjør vi mer skade enn nytte. Tilsvarende, hvis pretestsannsynlighet er over en viss terskel (T2), bør vi behandle uten å teste, fordi selv et negativt resultat ikke vil redusere sannsynlighet for sykdom til en verdi som ligger under behandlingsterskelen. Hvis vi da lar være å behandle på grunnlag av et negativt resultat, gjør vi mer skade enn nytte. Kun når pretestsannsynlighet ligger mellom de to tersklene, bør vi teste og behandle avhengig av testresultatet (6).

Kostnadseffektiv bruk av laboratorietester krever derfor at vi kan estimere både pretestsannsynlighet og behandlingsterskel.

2. Kontroll

I denne situasjon skal prøvesvarene hjelpe oss til å påvise eventuelle endringer hos pasienter med kjente helsetilstander. Da må vi kunne skille ut andre årsaker til endret prøveresultat. De kan deles inn i tre grupper:

• Preanalytiske faktorer
• Analytiske faktorer
• Normale biologiske endringer

Preanalytiske faktorer

Dette gjelder faktorer som forberedelse av pasient til prøvetaking, selve prøvetakingen og behandling av prøven før analyse. De viktigste faktorene er:

• Matinntak
• Kaffeinholdige drikker
• Røyking
• Alkohol
• Legemidler
• Kroppsaktivitet
• Kroppsstilling under prøvetaking
• Prøvetakingsteknikk
• Prøvemateriale
• Prøveoppbevaring

Det er vanskelig å eliminere effekten av preanalytiske faktorer, men så langt det er mulig, må pasienten være forberedt på samme måte til hver prøvetaking, og prøvene må tas og oppbevares forskriftsmessig hver gang. For eksempel vil det være villedende å måle b-hemoglobin hos en pasient som en gang er sengeliggende og neste gang er stående. Når en person reiser seg fra liggende til stående stilling, vil konsentrasjonen av celle- og proteinbundne substanser stige med 8-10 % etter ca. 10 minutter.

Analytiske faktorer

Utføring av analysen er selvsagt viktig. Vi bruker to mål for hvor korrekt en analyse er: Upresisjon og riktighet.

Upresisjon er et uttrykk for spredning av prøveresultater ved gjentatt analysering av samme prøve, og blir ofte oppgitt som en variasjonskoeffisient, som er standardavviket i prosent av gjennomsnittet. I omtalen av de enkelte analyser og undersøkelser har vi for kvantitative analyser oppgitt en analytisk variasjonskoeffisient. Den er beregnet på grunnlag av gjentatt analysering av samme prøve over et tidsrom på ca. ett år. Bare ett resultat per analyseserie (dag) er tatt med. Variasjonskoeffisienten gjelder for tilhørende nivå (konsentrasjon), og kan være større eller mindre i andre nivå. Så langt det har vært praktisk mulig, har vi brukt prøver som er behandlet på samme måten som vanlige pasientprøver. For eksempel er den analytiske variasjonskoeffisienten til b-HbA1c oppgitt til 3,2% ved et nivå på 5,7%. Hvis en tenkt pasient med b-HbA1c konstant lik 5,7% får målt b-HbA1c mange ganger i løpet av ett år, vil vi forvente at 95% av resultatene ligger i området 5,7% +/- 2 standardavvik, dvs. i området 5,3-6,1%, som følge av den analytiske variasjon alene. Men i tillegg til den analytiske variasjon kommer normal biologisk variasjon og eventuelle endringer som skyldes endret klinisk tilstand, se nedenfor.

Riktighet er et uttrykk for at prøveresultatet gjennomsnittlig ligger i riktig nivå, dvs. at analysen er riktig kalibrert og spesifikk (at den ikke måler noe annet enn den skal). Vi prøver alltid å kalibrere våre analysemetoder slik at resultatene gjennomsnittlig ligger i riktig nivå, dvs. i riktig nivå i forhold til de referansegrensene vi oppgir. Men vær oppmerksom på at analysemetoder ved andre laboratorier kan være kalibrert til et annet nivå, som er riktig for deres referansegrenser.

Normale biologiske endringer

En rekke normale forhold påvirker prøveresultatene, som for eksempel:
•Alder
•Kjønn
•Kroppsmasse
•Biologiske rytmer

Når vi har gjort rede for slike kjente årsaker til endringer i konsentrasjonen av ulike substanser, står vi tilbake med endringer som best kan kalles tilfeldige. Det betyr at det ikke er noe regelmessig mønster i endringene, og det er heller ikke noen grunn til å hevde at endrede stoffskifte­prosesser ligger under. Endringene kan best beskrives som tilfeldig fluktuasjon rundt et gjennomsnitt, og kan antas å følge en Gauss-fordeling (7). Denne tilfeldige variasjon i konsentrasjon av en substans hos samme person kalles intraindividuell biologisk variasjon.

Hos friske personer har vi etter hvert fått en del data om tilfeldig intraindividuell biologisk variasjon, både hos yngre og eldre. Ved en undersøkelse ble det funnet samme tilfeldige intraindividuelle biologiske variasjon for en del analyser i en gruppe eldre (70-83 år) som i en gruppe yngre (20-53 år) individer (8). Hos syke har vi mindre data, men det har vært gjort studier på pasienter med ulike stabi­le sykdomstilstander som kronisk nyre­svikt, essensiell hyper­tensjon, diabetes mellitus og kroniske leversykdommer. Disse undersøkelsene har vist at tilfeldig intra­individuell biologisk variasjon er av samme størrelse hos syke som hos friske, selv om de syke har verdier i et annet nivå. Tilsva­rende funn er gjort hos gravide. Men hos akutt syke pasienter er intraindividuell biologisk variasjon større enn hos friske (7).

I omtalen av de enkelte analyser og undersøkelser har vi oppgitt tilfeldig intra­individuell biologisk variasjon der denne er kjent. Disse tallene er mediane varia­sjonskoeffisienter, hentet fra referanse 1, som oppdatert i www.westgard.com/biodatabase1.htm, og supplert med data fra blant annet referanse 10. Hos den enkelte pasient kan variasjons­koeffisientene være mindre eller større. For analyser der intra­individuell biologisk variasjon er kjent, har vi også oppgitt en totalvariasjon, utregnet som

SD_total=(SD²_analytisk+SD²_biologisk)^0,5

Er sykdomsprosess årsak til endret prøveresultat?

Når vi sammenligner 2 prøveresultater tatt på ulike tidspunkter, skal vi vurdere om preanalytiske faktorer, analytiske faktorer og normal biologisk variasjon kan forklare forskjellen, eller om en reell endring i pasientens tilstand har funnet sted.

Under forutsetning av at preanalytiske faktorer er uendret, og at det ikke har funnet sted andre normale biologiske endringer enn de tilfeldige, kan vi som en grov tilnærming sette at (SD betyr standardavvik):

SD_total=(SD²_analytisk+SD²_biologisk)^0,5

SD_diff = (2•SD²_total)^0,5=1,414•SD_total

der SD_diff er standardavviket til differansen mellom to prøveresultater.

Undersøker vi differansen mellom to prøveresultater mange ganger, antar vi at verdiene fordeler seg som en Gauss-fordeling med gjennomsnitt lik 0 og standardavvik lik SD_diff. Hvis vi krever minst 95 % sannsynlighet for at forskjellen mellom to prøveresultater skyldes endringer i pasientens tilstand, krever vi at tallverdien til differansen mellom resultatene er minst 1,96•SD_diff, fordi det er bare 5 % sannsynlighet for å få en så stor, eller større, tallverdi  på grunn av analytiske faktorer og tilfeldig intraindividuell biologisk variasjon. Omregnet til SD_total blir det 1,96• SD_diff =1,96•1,414•SD_total = 2,8•SD_total. Nøyer vi oss med minst 90 % sannsynlighet, er det nok at differansen er minst 1,65•SD_diff =1,65•1,414•SD_total = 2,3•SD_total.

Et eksempel: Totalvariasjonen for b-HbA1c er oppgitt til 4,4 %. Hvis du vil være 95 % sikker på at en forskjell mellom 2 prøveresultater ikke bare skyldes tilfeldig variasjon (analytisk og biologisk), må forskjellen være minst 2,8•SD_total =2,8•4,4% = 12,3%. Hvis pasientens første prøvesvar var b-HbA1c=7 %, må det andre prøvesvaret være mindre enn 7% - (12,3/100)•7% = 6,1%, eller større enn 7% + (12,3/100)•7% = 7,9% for at du kan være 95% sikker på at forskjellen ikke bare skyldes tilfeldig variasjon (analytisk og biologisk).

Denne tankegangen kan si noe om sannsynligheten for at en endring i pasientens tilstand har funnet sted. Men regnestykket sier ingenting om endringen har klinisk betyding. Og omvendt - klinisk betydningsfulle endringer i pasientens tilstand kan selvsagt finne sted uten at vi påviser statistisk signifikante forskjeller mellom to prøveresultater.

Skal vi vurdere endringer på grunnlag av mer enn to prøveresultater, kan vi ikke bruke den enkle modellen som er nevnt over. Det finnes statistiske metoder som er beregnet for vurdering av seriemålinger med mer enn to resultater, men de er tungvinte å bruke, så vi har ingen praktiske alternativer til den gamle "øyemål-metoden", det vil si erfaring om hva som er betydningsfulle endringer. En spesiell situasjon er seriemåling av kreftmarkør for å vurdere om svulstfjerning har vært vellykket og for tidlig å oppdage residiv. Da kan vi ha nytte av matematiske modeller som beskriver endring av kreftmarkørens konsentrasjon hos pasienter med kjente sykdomsforløp. Slik endring kan for eksempel tallfestes som halveringstid og fordoblingstid (11, 12).